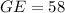Ok, so
Here we have the following segments:
We want to find the value of the measure of GE.
Notice that we have that:

If we look at the graph, we can see that the measure of GF can be found if we substract HF and HG. Right?
Therefore, GF will be:
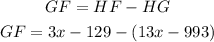
Multiplying the sign per the terms inside the brackets, we got that:

And, the segment GE can be found if we sum GF and FE.
This is:
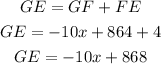
Now, we can see that GE is also given by the equation 3x - 185. So, we could equal both equations:
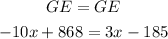
And if we solve this equation for x:
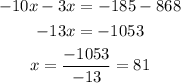
Now, we know that x=81.
To find the measure of GE, we just replace x=81 in any of both equations given for GE. We could replace in the second one because it is easier.

Therefore,