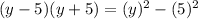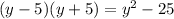Given the polynomial expression:
(y + 5)²
(y - 5)(y + 5)
Let's simplify each of the given expression:
a.) (y + 5)²
The given equation is a factor of a perfect square trinomial. For this type of expression, the following is the formula for expanding it.
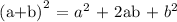
We get,
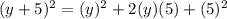
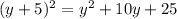
b.) (y - 5)(y + 5)
To be able to simplify the following expression. We will be using the formula for the difference of two squares.
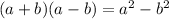
We get,