To determine the probability of independent P(A and B):
P(not A) = 0.6

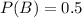
As they are independent, product of their probabilities is the probability of occurring of both events simultaneously i.e.
P(A and B)=P(A)*P(B)
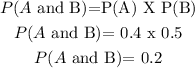
Therefore the probability of event A and B : P(A and B) = 0.2