Question

the graph represents Billy's speed on a recent trip . for which time. Is his rate of change negative? A. between 0 and 5 minutes B. between 5 and 10 minutes C. between 10 and 20 minutes D. between 20 and 25 minutes

Answer 1

D.between 20 and 25 minutes ​

Step-by-step explanation

Step 1

when you have 2 points of a lines, you can find the rate of change, using:

`\begin{gathered} \text{rate of change= slope=}(y_2-y_1)/(x_2-x_1) \\ \text{where } \\ P1(x_1,y_1) \\ P2(x_2,y_2) \end{gathered}`

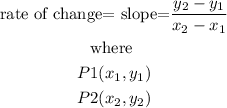
then

a) between 0 and 5 minutes

Let

P1(0,0)

P2(5,40)

apply the formula

`rate_1=(y_2-y_1)/(x_2-x_1)=(40-0)/(5-0)=(40)/(5)=8`

b)between 5 and 10 minutes

Let

P1(5,40)

P2(10,50)

apply

`rate_{2_{}}=(y_2-y_1)/(x_2-x_1)=(50-40)/(10-5)=(10)/(5)=2\text{ }`

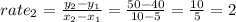
c)between 10 and 20 minutes

Let

P1(10,50)

P2(20,50)

apply

`\begin{gathered} rate_{3_{}}=(50-50)/(20-10)=(0)/(10)=0 \\ \end{gathered}`

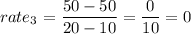
d)between 20 and 25 minutes ​

Let

P1(20,50)

P2(25,40)

apply

`\begin{gathered} rate_{4_{}}=(y_2-y_1)/(x_2-x_1)=(40-50)/(25-20)=(-10)/(5)=-2\Rightarrow negative \\ \end{gathered}`

so, the answer is D.between 20 and 25 minutes ​