The geometric series is;
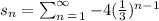
when n=1, we have
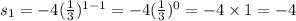
When n=2, we have,
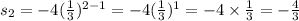
When n = 3, we get,
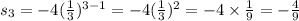
when n = 4, we get,

a. So, the first four terms of the series are: - 4, -4/3, -4/9 and -4/27
The sum to infinity of the series is:
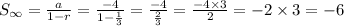
b. The series, as we can see, is CONVERGENT, because it has a definite value as its sum.
c. The sum of the series is - 6