Question

2. On a circle of radius 5 feet, what angle would subtend an arc of length 2 feet? Express your answer in both radians and degrees.

Answer 1

In radians, it is 2/5 radians

In degrees, it is 11.5 degrees

Step-by-step explanation:

radius = 5 feet

arc length = 2 feet

The formula relating the radius and the arc length is given as:

`\begin{gathered} s\text{ = r}\theta \\ \text{where s = arc length} \\ r=radius\text{ } \end{gathered}`
`\begin{gathered} \text{substitute the values:} \\ \text{ 2 = 5}\theta \\ \text{divide through by 5:} \\ (2)/(5)\text{ = }\theta \\ \\ In\text{ radians, }\theta\text{ = 2/5} \end{gathered}`

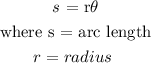
We will convert from radians to degrees:

`\begin{gathered} 1\text{ }\pi\text{ rad = 180 degr}ees \\ (2)/(5)rad\text{ = }(2)/(5)\text{ rad}*\frac{180\text{ degr}ees}{\pi\text{ rad}} \\ \\ =\text{ }\frac{36\text{ degr}ees}{\pi\text{ }} \\ =\text{ }11.5\text{ degr}ees \end{gathered}`

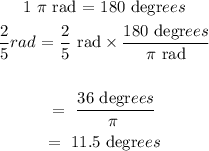
In radians, it is 2/5 radians

In degrees, it is 11.5 degrees