In radians, it is 2/5 radians
In degrees, it is 11.5 degrees
Step-by-step explanation:
radius = 5 feet
arc length = 2 feet
The formula relating the radius and the arc length is given as:
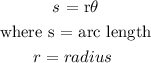

We will convert from radians to degrees:
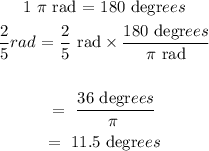
In radians, it is 2/5 radians
In degrees, it is 11.5 degrees