Answer:
4.78 m/s²
Step-by-step explanation:
First, we need to calculate the gravity of the planet, so we need to divide the weight by the mass to get:
g = W/m = 180N/55 kg = 3.27 m/s
Then, the range of the leap and the initial speed are related with the following equation
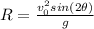
Where θ is the initial angle, g is the gravity and V0 is the initial velocity. Solving for V0, we get:
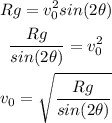
Finally, we can replace R = 3.5 m, g = 3.27 m/s², and θ = 15° to get:
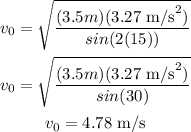
Therefore, the answer is 4.78 m/s²