Question

A 55 kg astronaut who weighs 180 N on a distant planet ispondering whether she can leap over a 3.5-m-wide chasm without falling in. If she leaps at a 15° angle, what initial speed doesshe need to clear the chasm?

Answer 1

4.78 m/s²

Step-by-step explanation:

First, we need to calculate the gravity of the planet, so we need to divide the weight by the mass to get:

g = W/m = 180N/55 kg = 3.27 m/s

Then, the range of the leap and the initial speed are related with the following equation

`R=(v_0^2sin(2\theta))/(g)`

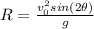
Where θ is the initial angle, g is the gravity and V0 is the initial velocity. Solving for V0, we get:

`\begin{gathered} Rg=v_0^2sin(2\theta) \\ (Rg)/(sin(2\theta))=v_0^2 \\ v_0=\sqrt{(Rg)/(sin(2\theta))} \end{gathered}`

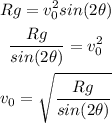
Finally, we can replace R = 3.5 m, g = 3.27 m/s², and θ = 15° to get:

`\begin{gathered} v_0=\sqrt{\frac{(3.5m)(3.27\text{ m/s}^2)}{sin(2(15))}} \\ v_0=\sqrt{\frac{(3.5m)(3.27\text{ m/s}^2)}{sin(30)}} \\ v_0=4.78\text{ m/s} \end{gathered}`

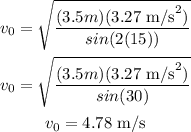
Therefore, the answer is 4.78 m/s²