Question

Please answer the question shown, and all of the boxes.

Options for box 1: Yes No
Box 2: Adjacent Vertical
Box 3 180 degrees 90 degrees
Box 4 Supplementary Complementary
Box 5 180 deg, 90 deg, 270 deg
Box 6 ,m∠9 < m∠6 + m∠8, m∠9 = m∠6 + m∠8, m∠9 > m∠6 + m∠8
Please help!!! 100 POINTS PLEASE

Answer 1

`\boxed{\sf Yes}\;;\textsf{because $\angle 9$ and $\angle7$ are \boxed{\sf vertical} angles, $m \angle 9=$ \boxed{\sf 90\; degrees}}\;.`

`\textsf{Because $\angle6$ and $\angle8$ are \boxed{\sf complementary} angles, $m\angle6+m\angle8=$\;\boxed{\sf 90\;degrees}}\;.`

`\textsf{Thus}, \; \boxed{\sf m\angle9 = m\angle6 + m\angle8}\;.`

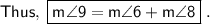
Explanation:

Vertical Angles Theorem

When two straight lines intersect, the opposite vertical angles are congruent.

Therefore, ∠9 and ∠7 are vertical angles and:

⇒ m∠9 = m∠7 = 90°

Angles on a straight line sum to 180°

⇒ m∠6 + m∠8 + m∠7 = 180°

⇒ m∠6 + m∠8 + 90° = 180°

⇒ m∠6 + m∠8 = 90°

Complementary Angles

Two angles whose measures sum to 90°.

Therefore, ∠6 and ∠8 are complementary angles and:

⇒ m∠6 + m∠8 = 90°

As m∠9 = 90° and m∠6 + m∠8 = 90° then:

⇒ m∠6 + m∠8 = m∠9