Answer:


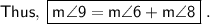
Explanation:
Vertical Angles Theorem
When two straight lines intersect, the opposite vertical angles are congruent.
Therefore, ∠9 and ∠7 are vertical angles and:
⇒ m∠9 = m∠7 = 90°
Angles on a straight line sum to 180°
⇒ m∠6 + m∠8 + m∠7 = 180°
⇒ m∠6 + m∠8 + 90° = 180°
⇒ m∠6 + m∠8 = 90°
Complementary Angles
Two angles whose measures sum to 90°.
Therefore, ∠6 and ∠8 are complementary angles and:
⇒ m∠6 + m∠8 = 90°
As m∠9 = 90° and m∠6 + m∠8 = 90° then:
⇒ m∠6 + m∠8 = m∠9