Question

At a large company, the Director of Research found that the average work time lost by employees due to accidents was 91 hours per year. She used a random sample of 21 employees. The standard deviation of the sample was 5.7 hours. Estimate the population mean for the number of hours lost due to accidents for the company, using a 99% confidence interval. Assume the variable is normally distributed. Round intermediate answers to at least three decimal places. Round your final answers to the nearest whole number.

Answer 1

The mean value of the population is 105

Explanation:

According to the question, we were given the following parameters

Given parameters:

Random sample = 21 employees

standard deviation = 5.7 hours

Confidence interval = 99%

Mean=?

The mean can be calculated using the below formula

`\begin{gathered} z\text{ }=\text{ x - }(\mu)/(s) \\ \text{where} \\ z\text{ = z-score} \\ \mu\text{ = mean} \\ s\text{ = standard deviation} \end{gathered}`

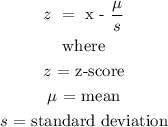
The z- score for 99% confidence interval = 2.576

The next thing is to substitute the above parameters into the formula

`\begin{gathered} 2.576\text{ = 21 - }(\mu)/(5.7) \\ \text{ Find the common denominator} \\ CD\text{ = 5.7} \\ 2.576=\text{ }\frac{21\cdot\text{ 5.7 - }\mu}{5.7} \\ 2.576\text{ = }\frac{119.7-\text{ }\mu}{5.7} \\ \text{cross multiply} \\ 2.576\cdot\text{ 5.7 = 119.7 - }\mu \\ 14.6832\text{ = 119.7 - }\mu \\ \text{Substract 119.7 from both sides} \\ 14.6832\text{ - 119.7 = -}\mu \\ -105.0168\text{ = -}\mu \\ \mu\text{ = 105} \end{gathered}`

Hence, the mean value of the population is 105