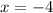Question

Consider the function g(x) = 1/2(x-3)(x+11) what is the equation of the axis of symmetry

Answer 1

Since the function represents a parabola (because it's a quadratic polynomial) we know that the axis of symmetry passes through the vertex and then we need to find the vertex of the function. To do that we write it in vertex form:

`g(x)=a(x-h)+k`

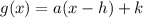
where (h,k) is the vertex. Let's write the function by completing the squares on x; then we have the form we need:

`\begin{gathered} g(x)=(1)/(2)(x-3)(x+11) \\ =(1)/(2)(x^2+11x-3x-33) \\ =(1)/(2)(x^2+8x-33) \\ =(1)/(2)(x^2+8x)-(33)/(2) \\ =(1)/(2)(x^2+8x+4^2)-(33)/(2)-(4^2)/(2) \\ =(1)/(2)(x+4)^2-(49)/(2) \end{gathered}`

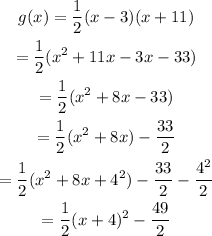
Comparing the last line with the general expression we notice that:

`\begin{gathered} h=-4 \\ k=-(49)/(2) \end{gathered}`

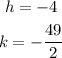
Hence the vertex is the point (-4,-49/2). Now that we have the vertex we have to remember that for a vertical parabola (as the one represented for the function) the axis of symmetry is given by:

`x=h`

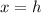
Therefore the axis of symmetry in this case is:

`x=-4`