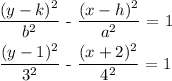Question

Write the equation of the hyperbola in standard form that satisfies the given conditions: Show all work.Center: (-2, 1)One Focus: (-2, 6)One Vertex: (-2, 4)

Answer 1

`((y-1)^2)/(3^2)\text{ - }((x+2)^2)/(4^2)`

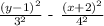
Explanation:

Given information

Center . (-2, 1)

One focus. (-2, 6)

One vertex. (-2, 4)

Recall that, the standard form of a hyperbola function is given below as

`\frac{(y\text{ - }k)^2}{b^2}-\text{ }((x-h)^2)/(a^2)=\text{ 1}`

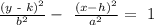
where (h,k) is the center of the circle

The next process is to determine the value of h and k

`\begin{gathered} Recall\text{ that, the center of the hyperbola is (-2, 1)} \\ Therefore,\text{ h = -2 and k = 1} \end{gathered}`

The next step is to determine the value of b by finding the distance between the center and the vertex

`\begin{gathered} \text{Center = (-2, 1) and vertex = (-2, 4)} \\ \text{Distance = }\sqrt[]{(x1-x2)^2+(y1-y2)^2} \\ \text{From the given points, let x1 = -2, y1 = 1, x2 = -2 and y2 = 4} \\ Recall\text{ that, the distance betwe}en\text{ the center and vertex = b} \\ b\text{ = }\sqrt[]{(-2+2)^2+(1-4)^2} \\ b\text{ = }\sqrt[]{0^2+(-3)^2} \\ b\text{ = }\sqrt[]{0\text{ + 9}} \\ b\text{ = }\sqrt[]{9} \\ b\text{ = 3} \end{gathered}`

The next step is to find the value of a using the below formula

`a^2\text{ = }b^2(e^2\text{ - 1)}`

To get the value of a, we need to get the value of e by finding the distance between the center and the focus

Let the distance between the center and the focus be CF

`\begin{gathered} \text{Center = (-2, 1) and focus = (-2, 6)} \\ \text{Distance = }\sqrt[]{(x1-x2)^2+(y1-y2)^2} \\ \text{From the given points, let x1 = -2, y1 = 1, x2 = -2 and y2 = 6} \\ CF\text{ = }\sqrt[]{(-2+2)^2+(1-6)^2} \\ \text{CF = }\sqrt[]{0^2+(-5)^2} \\ \text{CF = }\sqrt[]{0\text{ + 25}} \\ \text{CF= }\sqrt[]{25} \\ \text{CF= 5} \end{gathered}`

Recall that, CF = be

`\begin{gathered} \text{Recall that, b= 3, and CF = 5} \\ 5\text{ = 3 }\cdot\text{ e} \\ e\text{ = }(5)/(3) \end{gathered}`

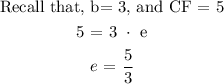
The next process is to determine the value of a from the below formula

`\begin{gathered} a^2=b^2(e^2\text{ - 1)} \\ a^2=3^2\text{ \lbrack(}(5)/(3))^2\text{ - 1)\rbrack} \\ a^2=3^2\text{ ( }(25)/(9)\text{ - 1)} \\ a^2=3^2\text{ (}\frac{25\text{ - 9}}{9}) \\ a^2\text{ = 9 (}(16)/(9)) \\ a^2\text{ = 16} \\ \text{Take the square roots of both sides} \\ \sqrt[]{a^2}\text{ = }\sqrt[]{16} \\ a\text{ = 4} \end{gathered}`

From the overall calculation, we were able to get the following values

h = -2

k = 1

b = 3

a = 4

The next process is to substitute the above value into the hyperbola formula

`\begin{gathered} ((y-k)^2)/(b^2)\text{ - }((x-h)^2)/(a^2)\text{ = 1} \\ ((y-1)^2)/(3^2)\text{ - }((x+2)^2)/(4^2)\text{ = 1} \end{gathered}`