Question

7. Pat and Chris both took a spatial abilities test (mean = 80, std dev. = 8). Pat scores a 76and Chris scored a 94. What proportion of individuals would score between Pat andChris?

Answer 1

Mean = 80

St Dev = 8

We take this as a normal distribution question.

First, the 68-95-99 rule.

The normal distribution is commonly associated with the 68-95-99 rule.

• 68% of the data is within 1 standard deviation (σ) of the mean (μ),

,

• 95% of the data is within 2 standard deviations (σ) of the mean (μ),

,

• and 99 of the data is within 3 standard deviations (σ) of the mean (μ).

Checking the two scores, it doesnt fall between any of the rules, so we need to convert to z scores.

The formula is:

`z=(x-\mu)/(\sigma)`

The first score (x) is 76, so corresponding z score is:

`\begin{gathered} z=(x-\mu)/(\sigma) \\ z=(76-80)/(8)=-.5 \end{gathered}`

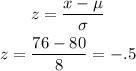
The second score is 94, this corresponds to:

`z=(94-80)/(8)=1.75`

This is:

We want the proportion (percentage).

Which is the blue shaded region.

If we use a normal table, we need:

z(1.75) - z(-0.5)

0.4599+0.1915 = 0.6514

In percentage, that is:

0.6514 * 100 = 65.14%

Hence, 65.14% of individuals would score between Pat and Chris.