Question

Tadeo has a bag of marbles with 5 blue marbles, 3 white marbles, and 5 red marbles.Find the following probabilities of Tadeo drawing the given marbles from the bag if the firstmarble(s) is (are) not returned to the bag after they are drawn. (Give your answer as a reducedfraction)a) A Blue, then a red-b) A red, then a white =c) A Blue, then a Blue, then a Blue =

Answer 1

Given:

5 blue marbles

3 white marbles

5 red marbles

TOTAL: 13 marbles in the bag

Solution:

a. Find the probability of picking a blue and then a red.

On the first pick, we know that there are 5 blue out of 13 marbles in the bag. On the second pick, there are 12 marbles left. Assuming that a blue marble was picked, there is now 5 red out of 12 marbles in the bag. So, the probability of picking a blue and then a red is:

`P(blue)* P(red)`
`(5)/(13)*(5)/(12)=(25)/(156)`

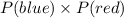
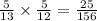
The probability of picking a blue and then a red is 25/156.

b. A red and then a white

In the same way as the previous one, we know originally that there were 5 red marbles out of 13 marbles in the bag. Assuming that red marble was picked, we know that there are now 3 white marbles out of 12 marbles for the second pick. So, the probability of picking a red and then a white is:

`(5)/(13)*(3)/(12)=(15)/(156)`

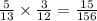
Reduce 15/156 by dividing both numerator and denominator by 3.

`(15/3)/(156/3)=(5)/(52)`

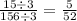
The probability of picking a red and then a white is 5/52.

c. A blue, then a blue, then a blue.

For the first pick, we have 5 blue marbles out of 13 marbles.

For the second pick, we now have 4 blue marbles out of 12 marbles.

For the third pick, we now have 3 blue marbles out of 11 marbles.

`(5)/(13)*(4)/(12)*(3)/(11)`
`(5)/(13)*(1)/(3)*(3)/(11)`
`(5)/(13)*(1)/(3)*(3)/(11)=(15)/(429)`

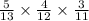
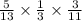
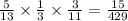
Reduced 15/429 by dividing both numerator and denominator by 3.

`(15/3)/(429/3)=(5)/(143)`

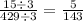
The probability of picking a blue, then a blue, then a blue is 5/143.