Question

Find the angle between u =(6,-5) and v= (11,8)

Answer 1

Dot product between vectors

We have two different kinds of products between vectors.

The dot product is given by two expressions:

`\begin{gathered} (1)\hat{u}\cdot\hat{v}=u_xv_x+u_yv_y \\ (2)\hat{u}\cdot\hat{v}=\hat|\hatv\cos \theta \end{gathered}`

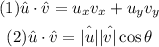
First expression

We have that

`\begin{gathered} \hat{u}=\langle u_x,u_y\rangle=\langle6,-5\rangle \\ \hat{v}=\langle v_x,v_y\rangle=\langle11,8\rangle \end{gathered}`

Then,

`\begin{gathered} u_x=6\text{ and }u_y=-5 \\ v_x=11\text{ and }v_y=8 \end{gathered}`

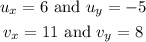
Then, for the first expression we have that:

`\begin{gathered} \hat{u}\cdot\hat{v}=u_xv_x+u_yv_y \\ \downarrow \\ \hat{u}\cdot\hat{v}=6\cdot11+(-5)\cdot8 \\ =66-40=26 \end{gathered}`

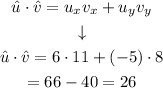
Then

`\hat{u}\cdot\hat{v}=26`

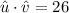
Second expression

We have that it can be expressed in another way. It will help us to find the answer:

`\hat{u}\cdot\hat{v}=\hatu|\hatv\cos \theta`

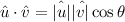
We have that

|u| and |v| are the magnitudes of each vector.

They are given by:

`\begin{gathered} \hat=\sqrt{u^2_x_{}+u^2_y} \\ |\hatv=√(v^2_x+v^2_y) \end{gathered}`

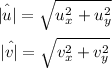
Then, we have that

`\begin{gathered} \hat=\sqrt{u^2_x_{}+u^2_y} \\ \downarrow\text{ since }u_x=6\text{ and }u_y=-5 \\ \hat=\sqrt[]{6^2+(-5)^2}=\sqrt[]{36+25}=\sqrt[]{61} \end{gathered}`

and

`\begin{gathered} \hat=\sqrt[]{v^2_x+v^2_y} \\ \downarrow\text{ since }v_x=11\text{ andv}_y=8 \\ \hat=\sqrt[]{11^2+8^2}=\sqrt[]{121+64}=\sqrt[]{185} \end{gathered}`

Then, using the second expression:

`\begin{gathered} \hat{u}\cdot\hat{v}=\hatu|\hatv\cos \theta \\ \downarrow \\ \hat{u}\cdot\hat{v}=\sqrt[]{61}\cdot\sqrt[]{185}\cos \theta=\sqrt[]{11,285}\cos \theta \end{gathered}`

Equation for the angle

Then, we have that both expressions are equal:

`\begin{gathered} \hat{u}\cdot\hat{v}=26 \\ \hat{u}\cdot\hat{v}=\sqrt[]{11,285}\cos \theta \end{gathered}`

Then,

`26=\sqrt[]{11,285}\cos \theta`

Using this equation we can find θ.

We solve this equation for θ by "leaving it alone" on the right isde of the equation:

`\begin{gathered} 26=\sqrt[]{11,285}\cos \theta \\ \downarrow\text{ taking }\sqrt[]{11,285}\text{ to the left side} \\ \frac{26}{\sqrt[]{11,285}}=\cos \theta \end{gathered}`

Using the calculator we have that:

`\begin{gathered} √(11,285)\cong106.23 \\ \downarrow \\ \frac{26}{\sqrt[]{11,285}}\cong(26)/(106.23)\cong0.244 \\ \downarrow \\ 0.244\cong\cos \theta \end{gathered}`

To solve the equation for θ, we take the cos to the left side of the equation using its inverse function arccos:

`\begin{gathered} 0.244\cong\cos \theta \\ \downarrow \\ \arccos (0.244)\cong\theta \end{gathered}`

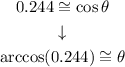
Using a calculator for arccos(0.244):

`\arccos (0.244)\cong75.83`

Then

θ ≅ 75.83º

Answer: the angle between the vectors is θ ≅ 75.83º