Dot product between vectors
We have two different kinds of products between vectors.
The dot product is given by two expressions:
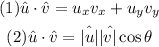
First expression
We have that
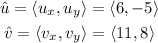
Then,
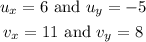
Then, for the first expression we have that:
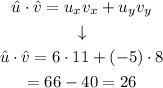
Then
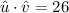
Second expression
We have that it can be expressed in another way. It will help us to find the answer:
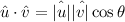
We have that
|u| and |v| are the magnitudes of each vector.
They are given by:
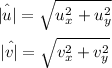
Then, we have that
![\begin{gathered} \hat=\sqrt{u^2_x_{}+u^2_y} \\ \downarrow\text{ since }u_x=6\text{ and }u_y=-5 \\ \hat=\sqrt[]{6^2+(-5)^2}=\sqrt[]{36+25}=\sqrt[]{61} \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/julesz7uzgf3z6xg9ozkpnm0m4zxpei2er.png)
and
![\begin{gathered} \hat=\sqrt[]{v^2_x+v^2_y} \\ \downarrow\text{ since }v_x=11\text{ andv}_y=8 \\ \hat=\sqrt[]{11^2+8^2}=\sqrt[]{121+64}=\sqrt[]{185} \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/j0y4t0x9puy55ruxhuzf9ws9xh5pd63wvr.png)
Then, using the second expression:
![\begin{gathered} \hat{u}\cdot\hat{v}=\hatu|\hatv\cos \theta \\ \downarrow \\ \hat{u}\cdot\hat{v}=\sqrt[]{61}\cdot\sqrt[]{185}\cos \theta=\sqrt[]{11,285}\cos \theta \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/yckm8bqshphs83lp49hukdu7ar2vdktahx.png)
Equation for the angle
Then, we have that both expressions are equal:
![\begin{gathered} \hat{u}\cdot\hat{v}=26 \\ \hat{u}\cdot\hat{v}=\sqrt[]{11,285}\cos \theta \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/d8sv381hkms2qapsv3fz8uhecq1rcapkr2.png)
Then,
![26=\sqrt[]{11,285}\cos \theta](https://img.qammunity.org/2023/formulas/mathematics/college/2bm27y1t4h2x7dhb9xw29f9qpbbemjw6wa.png)
Using this equation we can find θ.
We solve this equation for θ by "leaving it alone" on the right isde of the equation:
![\begin{gathered} 26=\sqrt[]{11,285}\cos \theta \\ \downarrow\text{ taking }\sqrt[]{11,285}\text{ to the left side} \\ \frac{26}{\sqrt[]{11,285}}=\cos \theta \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/mwtrh9hsi1lpzbc83x7no83rfexlhglrp1.png)
Using the calculator we have that:
![\begin{gathered} √(11,285)\cong106.23 \\ \downarrow \\ \frac{26}{\sqrt[]{11,285}}\cong(26)/(106.23)\cong0.244 \\ \downarrow \\ 0.244\cong\cos \theta \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/yft8d826r3lni7600xqwpf76z1rpxxp0vj.png)
To solve the equation for θ, we take the cos to the left side of the equation using its inverse function arccos:
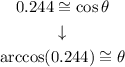
Using a calculator for arccos(0.244):
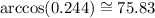
Then
θ ≅ 75.83º
Answer: the angle between the vectors is θ ≅ 75.83º