Given the resistors:
10Ω, 15 Ω and 20 Ω
Two resistors are connected in parallel and one in series.
Let's calculate all the possible total resistance values.
When resistors are connected in parallel, the equivalent resistance is:

After finding the equivalent resistance value in parellel, we now add the resistance value with the resistance in series:
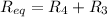
• When 10Ω and 15Ω are connected in parallel and 20Ω in series, we have:
R1 = 10 Ω
R2 = 15 Ω
R3 = 20 Ω
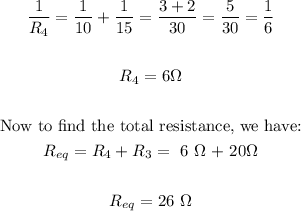
When 10Ω and 15Ω are connected in parallel and 20Ω in series the total resistance is 26 Ω.
• When 10Ω and 20Ω are connected in parallel and 15Ω in series, we have:
R1 = 10 Ω
R2 = 20 Ω
R3 = 15 Ω
Hence, we have:
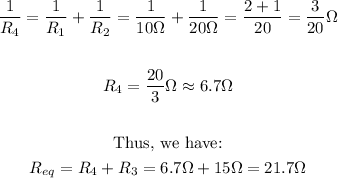
When 10Ω and 20Ω are connected in parallel and 15Ω in series the total resistance is 21.7 Ω.
• When 20Ω and 15Ω are connected in parallel and 10Ω in series, we have:
R1 = 20 Ω
R2 = 15 Ω
R3 = 10 Ω
Thus, we have:

When 20Ω and 15Ω are connected in parallel and 10Ω in series the total resistance is 18.6Ω.
ANSWER:
• When 10Ω and 15Ω are connected in parallel and 20Ω in series the total resistance is 26 Ω.
,
• When 10Ω and 20Ω are connected in parallel and 15Ω in series the total resistance is 21.7 Ω.
,
• When 20Ω and 15Ω are connected in parallel and 10Ω in series the total resistance is 18.6Ω.