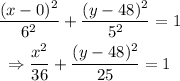The major axis measures 12 in, and the minor axis measures 10 in. The equation of an ellipse centered at (h, k) is given by the expression:
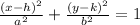
Where a is the measure of the semi-major(minor) axis, and b is the measure of the semi-minor(major) axis. In this case, the semi-major axis is horizontal (because it is 12 inches wide), so:
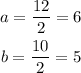
Now, if the center is at (0, 48), then h = 0 and k = 48. Using these values on the equation of the ellipse: