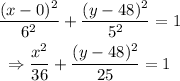Question

An elliptical mirror measures 12 inches wide and 10 inches high. The ellipse is centered at (0, 48) on a coordinate plane, where units are in inches. Which equation represents the mirror?

Answer 1

The major axis measures 12 in, and the minor axis measures 10 in. The equation of an ellipse centered at (h, k) is given by the expression:

`((x-h)^2)/(a^2)+((y-k)^2)/(b^2)=1`

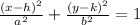
Where a is the measure of the semi-major(minor) axis, and b is the measure of the semi-minor(major) axis. In this case, the semi-major axis is horizontal (because it is 12 inches wide), so:

`\begin{gathered} a=(12)/(2)=6 \\ b=(10)/(2)=5 \end{gathered}`

Now, if the center is at (0, 48), then h = 0 and k = 48. Using these values on the equation of the ellipse:

`\begin{gathered} ((x-0)^2)/(6^2)+((y-48)^2)/(5^2)=1 \\ \Rightarrow(x^2)/(36)+((y-48)^2)/(25)=1 \end{gathered}`