Question

A 1420-kg car moving east at 17.0 m/s collides with a 1880-kg car moving south at 15.0 m/s, and the two cars connect together.A. What is the magnitude of the velocity of the cars right after the collision? (m/s )B. What is the direction of the cars right after the collision? Enter the angle in degrees where positive indicates north of east and negative indicates south of east. (°)C. How much kinetic energy was converted to another form during the collision? (kJ)

Answer 1

Given,

The mass of the car moving east, m=1420 kg

The mass of the car moving south, M=1880 kg

The velocity of the car moving east, u₁=17.0 m/s

The velocity of the car moving south, u₂=-15.0 m/s

Here we assume that the eastward direction is the positive x-direction and the southward direction is the negative y-direction.

From the law of conservation of momentum, the momentum is conserved in both directions simultaneously and independently.

Considering the conservation of momentum in the x-direction,

`mu_1=(m_{}+M)v_x`

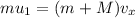
Where v_x is the x-component of the final velocity of the two cars.

On substituting the known values,

`\begin{gathered} 1420*17.0=(1420+1880)v_x \\ v_x=(1420*17.0)/((1420+1880)) \\ =7.32\text{ m/s} \end{gathered}`

Considering the conservation of momentum in the y-direction,

`Mu_2=(m+M_{})v_y`

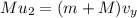
Where v_y is the y-component of the final velocity of the cars.

On substituting the known values,

`\begin{gathered} _{}1880*-15.0=(1420+1880)v_y \\ v_y=(1880*-15.0)/((1420+1880)) \\ =-8.55\text{ m/s} \end{gathered}`

A.

The magnitude of the velocity of the cars tight after the collision is given by,

`v=\sqrt[]{v^2_x+v^2_y}`

On substituting the known values,

`\begin{gathered} v=\sqrt[]{7.32^2+(-8.55)^2} \\ =11.26\text{ m/s} \end{gathered}`

Thus the magnitude of the velocity of the cars right after the collision is 11.25 m/s

B.

The direction of the cars right after the collision is given by,

`\theta=\tan ^(-1)((v_y)/(v_x))`

On substituting the known values,

`\begin{gathered} \theta=\tan ^(-1)((-8.55)/(7.32)) \\ =-49.4^(\circ) \end{gathered}`

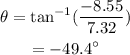
Thus the direction of the cars right after the collision is -49.4°. That is 49.4° south of the east.

C.

The total kinetic energy of the system is before the collision is

`K_1=(1)/(2)mu^2_1+(1)/(2)Mu^2_2`

On substituting the known values,

`\begin{gathered} K_1=(1)/(2)*1420*17.0^2+(1)/(2)*1880*15.0^2 \\ =205.19*10^3+211.5*10^3 \\ =416.69*10^3\text{ J} \end{gathered}`

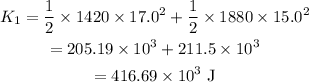
The kinetic energy of the system of two cars after the collision is,

`\begin{gathered} K_2=(1)/(2)(m+M)v^2 \\ =(1)/(2)*(1420+1880)11.26^2 \\ =209.2*10^3\text{ J} \end{gathered}`

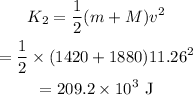
Thus the kinetic energy lost during the collision is,

`\Delta K_{}=K_1-K_2`

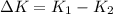
On substituting the known values,

`\begin{gathered} \Delta K=416.69*10^3-209.2*10^3 \\ =207.49*10^3\text{ J} \\ \approx207.5\text{ kJ} \end{gathered}`

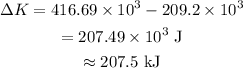
Thus the total kinetic energy lost during the collision is 207.5 kJ