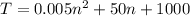SOLUTION:
We are told that the production cost is directly proportional to quantity.
Thus;
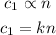
We are told that;
It costs $45,000 to produce 900 items, thus;
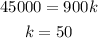
The cost to store n items varies as the square of n, thus;
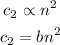
It costs $4050 to store 900 items, thus;
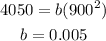
There is also a $1000 fixed daily cost; thus the total costs is;