We have the next points
H(-4,1)
I(-2,2)
J(-1,-2)
K(-4,-4)
The rule to rotate 180° counterclockwise
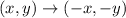
with rule, we can find the points
H'=(-(-4),-1)=(4,-1)
I'=(-(-2),-2)=(2,-2)
J'=(-(-1),-(-2))=(1,2)
K'=(-(-4),-(-4))=(4,4)
so the answer is
H'=(4,-1)
I'=(2,-2)
J'=(1,2)
K'=(4,4)
we can graph them they are the points in red