Airthemetic Sequence : arithmetic sequence is a sequence of numbers such that the difference between the consecutive terms is constant.
It express as :
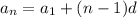
In the given question the 88 term is ( 25)
Substitute the value in the expression of n terms
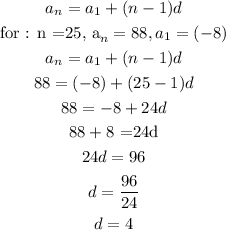
In the given Airthmetic sequence the constant difference, d = 4
Now for the position of term 8
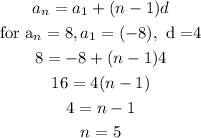
for n= 5 terms is 8
Now for the term of position 8:
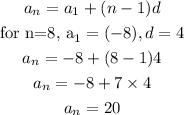
So, the term with position 8 is 20
Now for the position of term 36 :
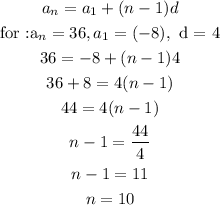
Thus, for n = 10, an = 36
Now, for the term of position 19
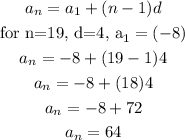
Thus at n = 19 the term i 64