We are given the following:
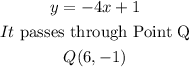
The general equation of a linear function is given by:
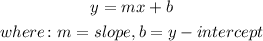
From the equations above, we deduce that:
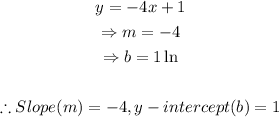
Two lines are considered parallel if they have an equal slope/gradient
We were given the Point Q. We will proceed to substitute the value of Q into the equation of the line. We have:

Therefore, the quation of the parallel line is }= - 4x+ 2 3$
Two lines are considered to be perpendicular if their slopes are the negative reciprocal of one other
Mathematically represented as:

The equation for the line perpendicular is given as:

Therefore, the equation of the parallel line is y = 1/4x - 5/2