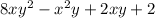Solution:
Given the polynomials below;
For the first polynomial
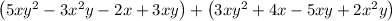
Adding the polynomials gives
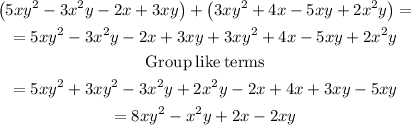
Hence, the matching polynomial is
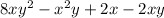
For the second polynomial
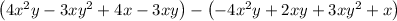
Subtracting the polynomials gives
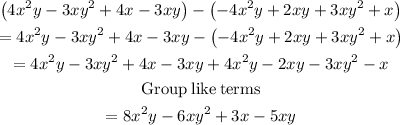
Hence, the matching polynomial is
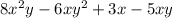
For the third polynomial
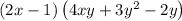
Multiplying the polynomials
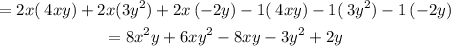
Hence, the matching polynomial is
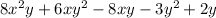
For the fourth polynomial
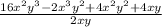
Dividing the polynomials
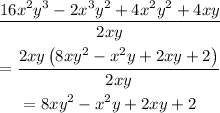
Hence, the matching polynomial is