Question

So this is the sinusoidal function (sine) with the height in meters, and time in seconds.

Answer 1

We have to find the equation of the water depth in function of time.

We will use the following function to model the water depth and then find all the parameters with the information given:

`d(t)=A\cdot\sin (Bt+C)+D`

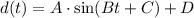
We know that the water depth is 8 m at low tide and 20 m at high tide.

This values give us the minimum and maximum values of the function.

The maximum value will happen when the sine function is equal to 1, so we can write:

`d_(\max )=A\cdot1+D=A+D=20`

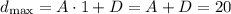
In the same way, we know that the minimum value of the function will happen when the sine function is equal to -1. Then, we can write:

`d_(\min )=A(-1)+D=-A+D=8`

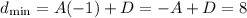
We now have a system of linear equations. We can solve for D by adding the two equations:

`\begin{gathered} (A+D)+(-A+D)=20+8 \\ A-A+D+D=28 \\ 2D=28 \\ D=(28)/(2) \\ D=14 \end{gathered}`

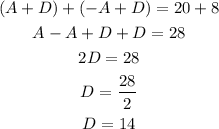
Now we can solve for A as:

`\begin{gathered} -A+D=8 \\ -A+14=8 \\ A=14-8 \\ A=6 \end{gathered}`

Then, we have two of the parameters already defined: A = 6 and D = 14.

Now, we use the fact that one cycle is completed after 12 hours. This means that the period is T = 12 hours.

The parameter B is the frequency, so it is equal to 2π/T. We then can write:

`B=(2\pi)/(T)=(2\pi)/(12)=(\pi)/(6)`

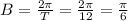
We now use the fact that the first high tide happens at 3:00 (t = 3).

This means that the sine function is equal to 1, when d(t) is maximum, at t = 3. Then we can write:

`\begin{gathered} d(3)=d_(\max ) \\ \sin ((\pi)/(6)(3)+C)=1 \\ \sin ((\pi)/(2)+C)=1 \\ (\pi)/(2)+C=(\pi)/(2) \\ C=0 \end{gathered}`

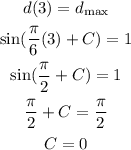
As the sine function is equal to 1 for π/2, the value of C is 0.

Then, we can write the complete function as:

`d(t)=6\cdot\sin ((\pi)/(6)t)+14`

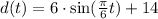
Now, we have to graph it for the first 48 hours.

This time represents 48/12 = 4 cycles.

As the phase is C = 0, the function starts at:

`d(0)=6\cdot\sin (0)+14=0+14=14`

Then, it will rise to a maximum at t = 3, as we know.

Then, it will pass through the average level of 14 m at t = 6.

The low tide will happen 3 hours later, at t = 9, when the depth will be d(9) = 8.

Finally, the cycle ends at t = 12, with a depth of 14 m.

We then can graph this as: