Question

How many gallons each of 30% alcohol and 5% alcohol should be mixed to obtain 25gal of 25% alcohol?

Answer 1

Let x be the amount of the 30% alcohol and let y be the amount of 5% alcohol.

We want the total amount to by 25 gal, then we have:

`x+y=25`

We also want the resulting mix to be 25% alcohol, this is 0.25 in decimal form; also we know that the first type of alcohol is 30% and the second is 5%, then we have:

`\begin{gathered} 0.3x+0.05y=0.25(25) \\ 0.3x+0.05y=6.25 \end{gathered}`

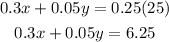
Hence we have the system of equations:

`\begin{gathered} x+y=25 \\ 0.3x+0.05y=6.25 \end{gathered}`

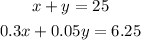
To solve the system we solve the first equation for y:

`y=25-x`

then we plug this value of y in the second equation:

`\begin{gathered} 0.3x+0.05(25-x)=6.25 \\ 0.3x+1.25-0.05x=6.25 \\ 0.25x=6.25-1.25 \\ 0.25x=5 \\ x=(5)/(0.25) \\ x=20 \end{gathered}`

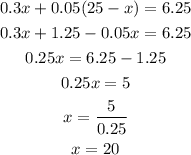
Once we have the value of x we plug it in the expression we found for y:

`\begin{gathered} y=25-20 \\ y=5 \end{gathered}`

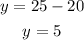
Therefore, the mixture will have 20 gallons of 30% alcohol and 5 gallons of 5% alcohol.