Given the function f(x) defined as:
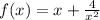
Taking the derivative of the function:
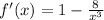
Now, we calculate the critical points using the equation:
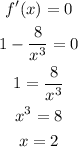
Now, we explore the intervals of increasing and decreasing for f(x) using the critical point, taking into account the discontinuity in x = 0:
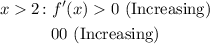
The intervals are:
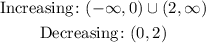
The function has a local minimum at x = 2, because f''(2) > 0. There is no local maximum.