This is the answers tab
Firstly, let us analyze the data the problem has given us. This can be achieved through a drawing
Given the equations of a movement with acceleration, we can write them as the following

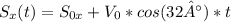
Given these equations and our data, we can replace some of its unknowns, and we're left with
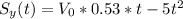
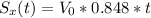
The first two equations were reduced to these ones by applying the data that the angle is 32°, and that the grenade hit at the same height. Now, we'll plug the information about the distance it reached. This will leave us with the following
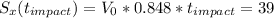
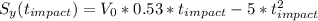
Then we're left with the following system

On our first equation, we can divide it by t impact, as we know it is not 0
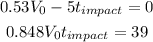
We can then rearrange and get the following
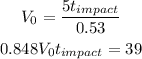
By replacing V0 on the lower equation, we get
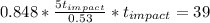
And this gives us the following equation
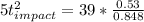
Simplifying...
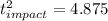
Finally, applying the square root, we're left with

So this is the time the Soldier had to escape