Question

A line through points (3,-12) and (13,8)Find the equation of the line

Answer 1

We have the two points: (3, -12) and (13,8)

To find the equation:

Step 1. Label the coordinates as follows:

`\begin{gathered} x_1=3 \\ y_1=-12 \\ x_2=13 \\ y_2=8 \end{gathered}`

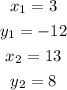
Step 2. Find the slope of the line with the slope formula:

`m=(y_2-y_2)/(x_2-x_1)`

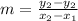
Substituting the values:

`m=(8-(-12))/(13-3)`

simplifying the result:

`\begin{gathered} m=(8+12)/(10) \\ m=(20)/(10) \\ m=2 \end{gathered}`

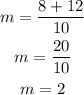
Step 3. Use point (x1,y1) which is (3,-12) and the slope m=2 in the point slope equation:

`y-y_1=m(x-x_1)`

Substituting the values:

`y-(-12)=2(x-3)`

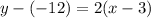
And we simplify to solve for y, also, we use distributive property on the right side to multiply 2 by x and 2 by -3:

`y+12=2x-6`

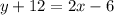
Finally, we substract 12 to both sides:

`\begin{gathered} y+12-12=2x-6-12 \\ y=2x-18 \end{gathered}`

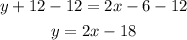
Answer: y=2x-18