Step-by-step explanation
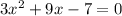
Esta es una funcion cuadratica, por lo que debemos obtener las raices de la misma.
![\frac{-b\pm\sqrt[]{b^2-4ac}}{2a}](https://img.qammunity.org/2023/formulas/mathematics/college/kaoalb540qnvy45obw509ttuwfskx00e99.png)
Aquí podemos ver que b=9, a=3 y c=-7, por lo que sustituyendo estos valores en la ecuación anterior, nos dará las raices de la función cuadráticaÑ
![x1,x2=\frac{-9\pm\sqrt[]{9^2-4\cdot3\cdot(-7)}}{2\cdot3}](https://img.qammunity.org/2023/formulas/mathematics/college/gnqmsv1ll796xbcambd7zf4uk3mecm6qvj.png)
Luego, resolviendo dicha ecuación tendremos que:
![x1,x2=\frac{-9\pm\sqrt[]{81+84}}{6}=\frac{-9\pm\sqrt[]{165}}{6}=](https://img.qammunity.org/2023/formulas/mathematics/college/vyax9crc5k5vmu6o83jbu3mj0ljrvh117i.png)
Las raices de este sistema serán irracionales:
Por lo tanto, la factorización de este sistema nos dará como resultado final:
![x_1=\frac{-9+\sqrt[]{165}}{6}\text{ x2=}\frac{-9-\sqrt[]{165}}{6}](https://img.qammunity.org/2023/formulas/mathematics/college/a5meusfip6mrphbpzh8mc4hzryw8iqlx82.png)
![3x^2+9x-7\text{ = (x-(}\frac{-9-\sqrt[]{165}}{6}\text{))(x-((}\frac{-9+\sqrt[]{165}}{6}\text{))}=0](https://img.qammunity.org/2023/formulas/mathematics/college/ybo1knz4qipzyouylt2por5ewtz3468srl.png)