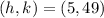We have the parabola equation in standard form:
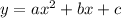
and we need to convert it into a vertex form:
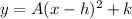
In order to obtain it, we can note that
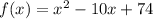
can be rewritten as
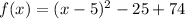
this is because
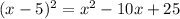
From our last result, we have
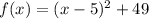
By comparing this result with the general vertex form, we can note that
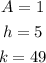
Therefore, the equation in vertex form is given by:
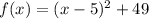
with vertex: