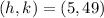Question

Find the vertex and write the quadratic function in vertex form (which our OpenStax textbook also calls the standard form).f(x)=x^2−10 x + 74 Give the vertex. Enter your answer as a point (a,b) .Vertex:Enter the coordinates of the vertex to write f(x) in vertex form:f(x)=(x− )^2+

Answer 1

We have the parabola equation in standard form:

`y=ax^2+bx+c`

and we need to convert it into a vertex form:

`y=A(x-h)^2+k`

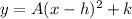
In order to obtain it, we can note that

`f(x)=x^2-10x+74`

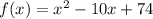
can be rewritten as

`f(x)=(x-5)^2-25+74`

this is because

`(x-5)^2=x^2-10x+25`

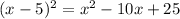
From our last result, we have

`f(x)=(x-5)^2+49`

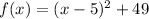
By comparing this result with the general vertex form, we can note that

`\begin{gathered} A=1 \\ h=5 \\ k=49 \end{gathered}`

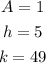
Therefore, the equation in vertex form is given by:

`f(x)=(x-5)^2+49`

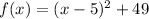
with vertex:

`(h,k)=(5,49)`