ANSWER:
The average cost per mile decreases
Explanation:
We have the following function:
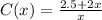
If we give value to x, we obtain the following:
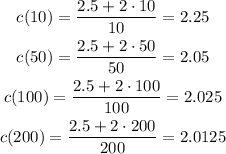
We can see that it is evident that as x increases, c (x) decreases. Depending on the situation, if we travel more miles, the average cost per mile decreases.