Question

Need to know the answers or how to do them.#1 please

Answer 1

Looking at angle G, it inscribes the arc FH, which is a diameter of the circle.

Since an inscribed angle measures half the inscribed arc (and arc FH measures 180°), angle G measures 90°.

Now, let's calculate angle F:

`\begin{gathered} F+G+H=180\\ \\ F+90+48=180\\ \\ F+138=180\\ \\ F=180-138\\ \\ F=42° \end{gathered}`

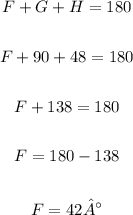
Arc GH is inscribed by the angle F, so we have:

`\begin{gathered} F=(1)/(2)GH\\ \\ 42=(1)/(2)GH\\ \\ GH=2\cdot42\\ \\ GH=84° \end{gathered}`

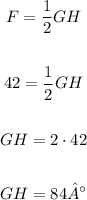
So the indicated arc measures 84°.