Question

suppose that the function g is defined, for all real numbers, as follows in the picture. find g(-2), g(0), and g(5)

Answer 1

We have to evaluate the piecewise defined function

`g(x)=\mleft\{\begin{aligned}-2\text{ }if\text{ x<-2} \\ (x-1)^2-2\text{ if -2}\leq x\leq2 \\ -(1)/(2)x+2\text{ if x>2}\end{aligned}\mright.`

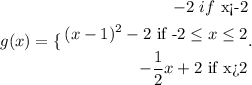
to evaluate this type of function we have to be careful to choose the right relation for the number we are evaluating.

Let's do the first one

`g(-2)`

Since the -2 lies in the second interval of the function we have to choose the second relation in the function, then

`\begin{gathered} g(-2)=(-2-1)^2-2 \\ =(-3)^2-2 \\ =9-2 \\ =7 \end{gathered}`

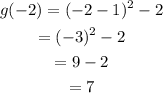
therefore g(-2)=7.

To evaluate g(0) we notice that x=0 also lies in the second interval of the piecewise function. Then

`\begin{gathered} g(0)=(0-1)^2-2 \\ =(-1)^2-2 \\ =1-2 \\ =-1 \end{gathered}`

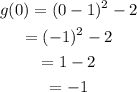
therefore g(0)=-1.

Finally, to evaluate g(5) we notice that x=5 lies in the third interval of the function, then

`\begin{gathered} g(5)=-(1)/(2)(5)+2 \\ =-(5)/(2)+2 \\ =-(1)/(2) \end{gathered}`

Therefore g(5)=-1/2.