Question

Find the six trigonometric functions of 0 in simplest radical form. Rationalize all fractions.

Answer 1

step 1

Find the hypotenuse of the right triangle

applying Pythagorean theorem

c^2=2^2+3^2

c^2=4+9

`c=\sqrt[]{13}`

step 2

Find sin(theta)

we have

`\sin (\theta)=\frac{2}{\sqrt[]{13}}`

simplify

`\sin (\theta)=\frac{2}{\sqrt[]{13}}=\frac{2\sqrt[\square]{13}}{13}`

opposite side divided by the hypotenuse

step 3

Find cos(theta)

`\cos (\theta)=\frac{3}{\sqrt[\square]{13}}`

adjacent side divided by the hypotenuse

simplify

`\cos (\theta)=\frac{3}{\sqrt[\square]{13}}=\frac{3\sqrt[]{13}}{13}`

step 4

find tan(theta)

`\tan (\theta)=(2)/(3)`

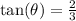
opposite side divided by the adjacent side

step 5

find cot(theta)

`\cot (\theta)=(1)/(\tan (\theta))=(3)/(2)`

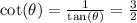
adjacent side divided by the opposite side

step 6

Find sec(theta)

`\sec (\theta)=(1)/(\cos (\theta))=\frac{\sqrt[]{13}}{3}`

hypotenuse divided by the adjacent side

step 7

Find csc(theta)

`\csc (\theta)=(1)/(\sin (\theta))=\frac{\sqrt[]{13}}{2}`

hypotenuse divided by the opposite side