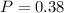Question

What is the probability that the random selection of the four-person group willresult in three math majors and 1 computer science major?

Answer 1

We have 18 students,

There are 11 math majors and 7 computer science majors.

We need to find the probability that randomly selecting four persons in the group will result in three math majors and 1 computer science major.

Now,

For select 3 math majors of 11, we use a combination:

11C3

Where the formula is given by:

`\text{nCr}=(n!)/((n-r)!r!)`

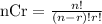
Where n is the number of the total group and r the sample:

Then:

`11C3=(11!)/(3(11-7)!)=165`

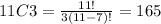
Now, for the selection 1 computer science major of 7:

n=7 and r=1

`7C1=(7!)/(1!(7-1)!)=7`

Now, the selection 4 persons of the group of 18 students:

18C4, where n=18 and r=4

`18C4=(18!)/(4!(18-4)!)=3060`

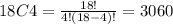
The probability of the chose three math majors and 1 computer science major, is given by:

`P=(7C1\cdot11C3)/(18C4)=(7\cdot165)/(3060)`

Therefore:

`P=0.38`