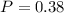We have 18 students,
There are 11 math majors and 7 computer science majors.
We need to find the probability that randomly selecting four persons in the group will result in three math majors and 1 computer science major.
Now,
For select 3 math majors of 11, we use a combination:
11C3
Where the formula is given by:
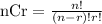
Where n is the number of the total group and r the sample:
Then:
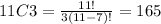
Now, for the selection 1 computer science major of 7:
n=7 and r=1
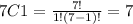
Now, the selection 4 persons of the group of 18 students:
18C4, where n=18 and r=4
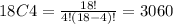
The probability of the chose three math majors and 1 computer science major, is given by:
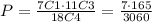
Therefore: