We want to find the equation of a line with slope -2/3 and goes through the point (-6,-5).
We can write the general equation of a line as:
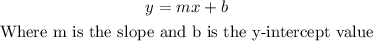
In this case, m=-2/3 and the point (-6,-5) must satisfy the equation, so:
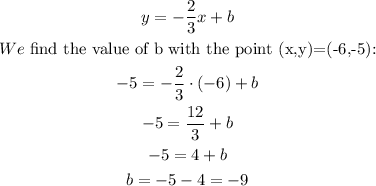
Now, we replace the value of b and write the equation in the standard form:
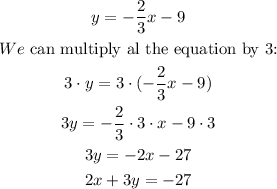
So, the option A is the correct answer.