Question

Write the equation of a line with slope of- 2/3and goes through the point (−6,−5)in standard form. A. 2x + 3y = -27B. -2x + 3y = -27C. 2x + 3y = -3D. -2x + 3y = 3

Answer 1

We want to find the equation of a line with slope -2/3 and goes through the point (-6,-5).

We can write the general equation of a line as:

`\begin{gathered} y=mx+b \\ \text{Where m is the slope and b is the y-intercept value} \end{gathered}`

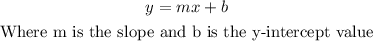
In this case, m=-2/3 and the point (-6,-5) must satisfy the equation, so:

`\begin{gathered} y=-(2)/(3)x+b \\ We\text{ find the value of b with the point (x,y)=(-6,-5):} \\ -5=-(2)/(3)\cdot(-6)+b \\ -5=(12)/(3)+b \\ -5=4+b \\ b=-5-4=-9 \end{gathered}`

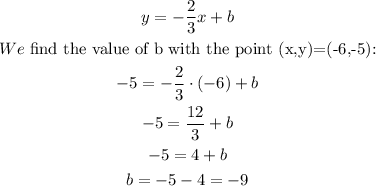
Now, we replace the value of b and write the equation in the standard form:

`\begin{gathered} y=-(2)/(3)x-9 \\ We\text{ can multiply al the equation by 3:} \\ 3\cdot y=3\cdot(-(2)/(3)x-9) \\ 3y=-(2)/(3)\cdot3\cdot x-9\cdot3 \\ 3y=-2x-27 \\ 2x+3y=-27 \end{gathered}`

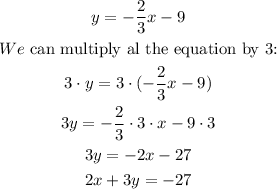
So, the option A is the correct answer.