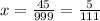Question

Find the fraction equivalent to 0.045045....

Answer 1

The fraction is 5/111

Step-by-step explanation

To find the fraction equivalent to a recurring decimal we have to follow these steps:

STEP 1: let 'x' be the recurring decimal:

`x=0.045045045\ldots`

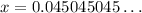
STEP 2: let 'n' be the number of recurring digits:

`n=3`

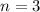
STEP 3: multiply the recurring decimal by 10^n:

`\begin{gathered} 10^3x=10^3\cdot0.045045045\ldots \\ 1000x=45.045045\ldots \end{gathered}`

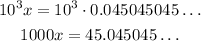
STEP 4: subtract the equation from step 1 from the equation from step 3:

`\begin{gathered} 1000x-x=45.045045045\ldots-0.045045045\ldots \\ 999x=45 \end{gathered}`

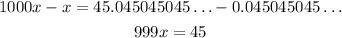
STEP 5: solve for x. Simplify the fraction if neccessary:

`x=(45)/(999)=(5)/(111)`