ANSWER
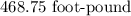
Step-by-step explanation
Let the bucket be lifted x feet.
The weight of the bucket at x feet is given by:
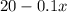
The work done in lifting the bucket by dx feet is:
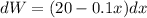
The total work done is the integral of the work done in lifting the bucket x feet, that is:
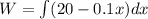
Hence, the work done in lifting the bucket 25feet is:
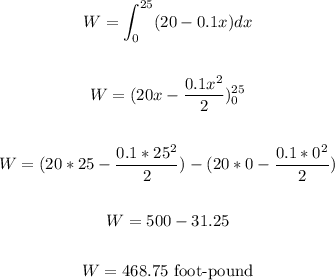
That is the answer.