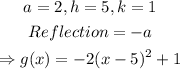Let's begin by identifying key information given to us:
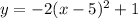
The general formula for the transformation is:
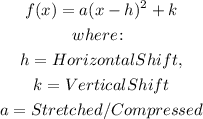
a)
Vertical Stretch by a factor of 2, shifts left 5units, shifts down 1 unit, and reflection gives:

b)
Vertical compression by a factor of 2, shifts right 5 units, shifts up 1 unit, and reflection across the x-axis gives:

c)
Vertical stretch by a factor of 2, shifts right units, shifts up 1 unit, and reflection across the x-axis gives: