Question

given a soda can with a volume of 36 and a diameter of 4 what is the volume of a cone that fits perfectly inside the soda can

Answer 1

Given:

The volume of the can, V=36.

The diameter of the can, D=4.

The can has the shape of a cylinder.

The radius of the can is,

`\begin{gathered} r=(D)/(2) \\ =(4)/(2) \\ =2 \end{gathered}`

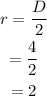
The equation for the volume of a cylinder is,

`V=\pi r^2h`

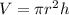
Here, h is the height of the cylinder.

The volume of a cone that fits perfectly inside a cylinder has the same radius and the same height as the cylinder

The equation for the volume of a cone is,

`V=(1)/(3)\pi r^2h`

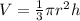
Therefore, the volume of the cone is 1/3 rd of the volume of the cylinder.

Hence, the volume of the cone can be found as,

`\begin{gathered} V_c=(V)/(3) \\ =(36)/(3) \\ =12 \end{gathered}`

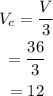
Therefore, the volume of the cone is 12.