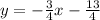Question

Find the equation of the line passing through the point (-7,2) that is perpendicular to the line 4x - 3y = 10

Answer 1

To write the equation of a line in the form y=mx+b you need to identify the slope (m) and the y-intercept (b).

Slope:

Two perpendicular lines have opposite reciprocals:

You have the line:

`4x-3y=10`

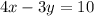
Identify the slope in the equation above (solve the equation for y to get a equation in the form y=mx+b):

`\begin{gathered} 4x-4x-3y=-4x+10 \\ -3y=-4x+10 \\ (-3)/(-3)y=(-4x)/(-3)+(10)/(-3) \\ \\ y=(4)/(3)x-(10)/(3) \end{gathered}`

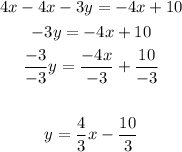
The slope of the perpendicular line (given) is 4/3.

Find the opposite reciprocal to find the slope of the line:

`\begin{gathered} m=-(1)/(m) \\ \\ m=-(1)/((4)/(3)) \\ \\ \\ m=-(3)/(4) \end{gathered}`Slope: -3/4

y-intercept:

Use the given point (-7,2) (x= -7 and y= 2) and the slope (m=-3/4) in the equation y=mx+b to solve b:

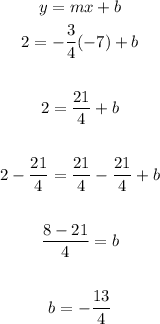
`\begin{gathered} y=mx+b \\ 2=-(3)/(4)(-7)+b \\ \\ 2=(21)/(4)+b \\ \\ 2-(21)/(4)=(21)/(4)-(21)/(4)+b \\ \\ (8-21)/(4)=b \\ \\ b=-(13)/(4) \end{gathered}`Y-intercept: -13/4Equation of the line:
`y=-(3)/(4)x-(13)/(4)`