The rate of change is the slope of the equation indicated as m in this formula:

where (x₁,y₁) and (x₂,y₂) are the coordinates of the points located in the table.
For the first option, let's use (x₁,y₁)=(3,-8) and (x₂,y₂)=(4,-5) as the two points on the graph. Substitute the coordinates into the equation and then simplify.
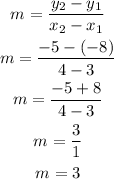
Since the slope is 3, the first option is incorrect.
For the second option, use the first two set of coordinates and then subtitute it to the formula. Simplify the expression.
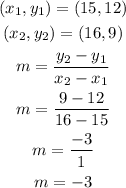
Since the slope is -3, let's check if the other set of coordinates will also result to a slope of -3. Let's use the second and the third set of coordinates.
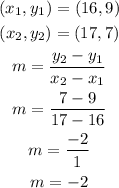
Since the slope is not equal to -3, the rate of change for the second option is not constant.
We may continue the process and check the value of the obtained m. The value must always be equal to -3. If one pair of set of coordinates will not result to -3, then the rate of change, or the slope, is not constant at -3.
To easily identify the answer, look at the values of x. As we can see, the values of x is constantly increasing by 1.
As for the value of y, since we need to obtain a negative slope, that means the value of y must decrease by 3 as x increases by 1.
From the options, only the last option, which is located at the right must part, has a value of y that decreases by 3 as the value of x increases by 1.
To check, substitute the value of the first two set of coordinates into the formula for the slope and check whether the value of the slope is -3.
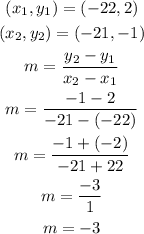
Now let's check the second and the third set of