Question

Which function below has the end behavior f(x) →-infinity as x → infinity and f (x) → infinity as x→-infinity

Answer 1

To find the function that has the following end behavior:

`\begin{gathered} f(x)\rightarrow-\infty\text{ as }x\rightarrow\infty \\ f(x)\rightarrow\infty\text{ as }x\rightarrow-\infty \end{gathered}`

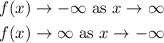
Considering the function which is given in option C.

When x tends to infinity,

`\begin{gathered} f\mleft(x\mright)=-x^3-4x^2+x \\ \lim _(x\to\infty)(-x^3-4x^2+x)=-\infty \\ \lim _(x\to-\infty)(-x^3-4x^2+x)=\infty \end{gathered}`

In other words, the degree of the given function is 3.

That is, odd.

The leading coefficient is -1.

That is, negative.

Hence, the end behavior is,

`\begin{gathered} f(x)\rightarrow-\infty\text{ as }x\rightarrow\infty \\ f(x)\rightarrow\infty\text{ as }x\rightarrow-\infty \end{gathered}`

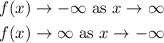
Hence, the correct option is C.